День математика

Этот День математики проводила в ЦБ,  пригласив преподавателей математики и учеников 11 б математического класса.

Выложила все материалы. Конечно, же, не все использовала. Пока готовишься столько перелопатишь! Выбирайте, применяйте!

 

Да здравствует математика!

Математику уже затем учить следует, что она ум в порядок приводит М. В. Ломоносов

ВЕДУЩИЙ:

Без счета не будет на улице света.

Без счета не может подняться ракета.

Без счета письмо не найдет адресата,

И в прятки сыграть не сумеют ребята.

Запомните все, что без точного счета

Не сдвинется с места любая работа!

 

Потреб­ности измерения (например, коли­чества зерна, длины дороги) привело человечество к появлению названий и обозна­чений простейших дробных чисел и к разработке приемов выполнения арифметических действий над дро­бями. Таким образом накапливался материал, который постепенно скла­дывался в древнейшую математичес­кую науку — арифметику. Измере­ние площадей и объемов, потребно­сти строительной техники, а несколько позднее — астрономии вызывают развитие начатков геомет­рии. Эти процессы шли у многих на­родов в значительной мере незави­симо и параллельно. Особенное зна­чение для дальнейшего развития науки имело накопление арифмети­ческих и геометрических знаний в «Египте и Вавилонии. В Вавилонии на основе развитой техники арифме­тических   вычислений   появились также начатки алгебры, а в связи с запросами астрономии — начатки тригонометрии. Так зарождалась ма­тематика. Сейчас самый обычный школьник знает намного больше, чем древний человек.

Математика — одна из древнейших наук. Дать краткое определение математики совсем не просто: 

• школьник на­чальных классов, только приступивший к изу­чению арифметики, скажет, что математика изучает правила счета предметов. И он будет прав, поскольку именно с этим он знакомится на первых порах.
• Школьники постарше доба­вят к сказанному, что в понятие математики входят алгебра и изучение геометрических объектов: линий, их пересечений, плоских фи­гур, геометрических тел, разного рода преобра­зований.
• Выпускники же средней школы включат в определение математики еще изу­чение функций и действие перехода к пределу, а также связанные с ним понятия произ­водной и интеграла.
• Выпускников университетов и пе­дагогических институтов уже не удовлетворят школьные определения, поскольку они знают, что в состав математики входят и другие дис­циплины: теория вероятностей, математичес­кая статистика, дифференциальное исчисле­ние, программирование для ЭВМ, вычисли­тельные методы, а также применения на­званных дисциплин для моделирования про­изводственных процессов, обработки опытных данных, передачи и обработки информации.

 

Однако и тем, что перечислено, не исчерпы­вается содержание математики.

 

Землемерие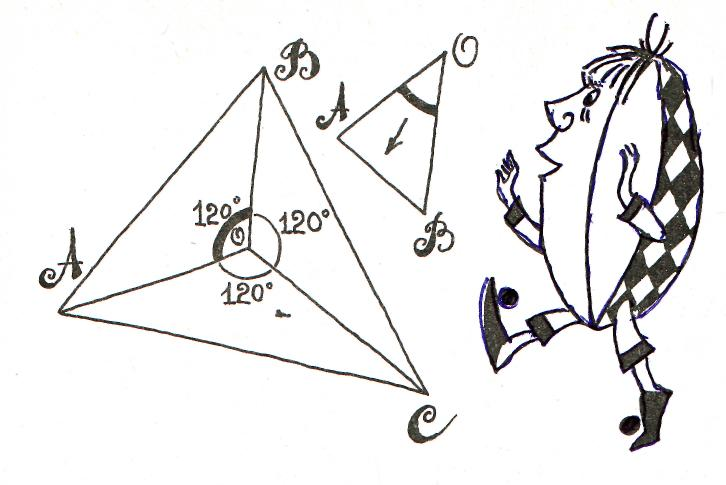  

 

 

Математика! Мир без нее был бы неинтересен. Без математики люди не соверши­ли бы научные открытия ни на море, ни на суше, ни во вселен­ной.

Давайте тоже совершим путе­шествие в мир занимательных за­дач, загадок и вопросов и назовем сегодняшний день – День математика!

А я рада приветствовать сегодня в зале внимательных и любознательных юных мате­матиков!

Сегодня вашему пытливому взору мы представили все математическое великолепие, которое хранится в нашей библиотеке. И знакомство с этой литературой, мы начнем пожалуй с того раздела, который поведает нам о людях, без которых не было бы математики!

В истории науки математики первым математиком принято называть ФАЛЕСА — греческого купца, путешественника и философа, жившего в 7  в. до н. э. Ему приписываются первые математические теоремы. Измерив, тень от египетской пирамиды и тень от шеста и применив свои теоремы о подобии, он вычислил высоту пи­рамиды.

ФАЛЕС в древности почи­тался как один из «Семи мудрецов».

 

ПИФАГОР

(ок. 570-ок. 500 гг. до н.э.)

Письменных документов о Пифагоре Самосском не осталось. Известно, что Пифагор покинул свой родной остров Самос в Эгейском море в знак протеста про­тив тирании правителя и уже в зре­лом возрасте (по преданию в 40 лет) появился в греческом городе Кро­тоне на юге Италии. Пифагор и его последователи — пифагорейцы — обра­зовали тайный союз, игравший не­малую роль в жизни греческих ко­лоний в Италии. Пифагорейцы узна­вали друг друга по звездчатому пя­тиугольнику — пентаграмме.

На учение Пифагора большое влия­ние оказала философия и религия Востока. Он много путешествовал по странам Востока: был в Египте и в Вавилоне. Там Пифагор позна­комился и с восточной математи­кой. Математика стала частью его учения, и важнейшей частью.

Пифагорейцы верили, что в число­вых закономерностях спрятана тай­на мира. Мир чисел жил для пи­фагорейца особой жизнью, числа име­ли свой особый жизненный смысл. Пи­фагор впервые разделил числа на четные и нечетные, простые и состав­ные, ввел понятие фигурного числа.

Естественно, что геометрия у Пи­фагора была подчинена арифметике, это ярко проявилось в теореме, но­сящей его имя и ставшей в даль­нейшем основой применения числен­ных методов в геометрии. (Позже Евклид вновь вывел на первое мес­то геометрию, подчинив ей алгебру.)

Следует заметить, что Пифагор считал Землю шаром, движущимся вокруг Солнца. Когда в XVI в. цер­ковь начала ожесточенно преследо­вать учение Коперника, это учение упорно именовалось пифагорейским.

 

Задачи альфабетагаммии

Перефразируем: современное – хорошо замаскированное древнее, отсюда вопрос: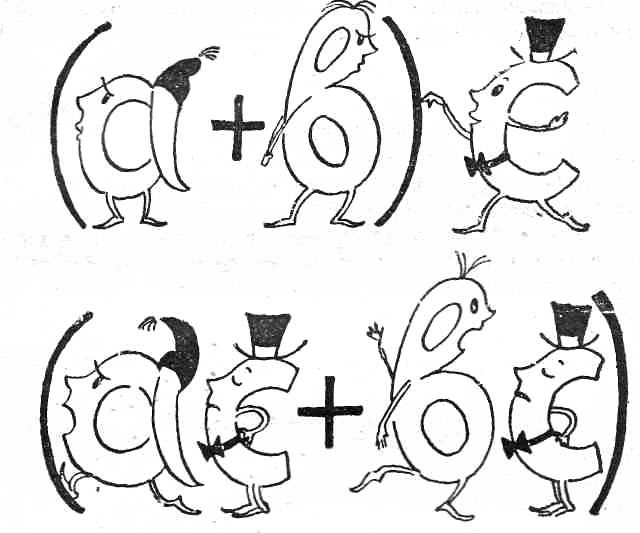

Кто знает что такое

 Гексаэдр  (куб)

Пентаграмм (это пятиконечная звезда. Ее можно получить, если продлить стороны пятиугольника.),

гексаг­рама (это шестиугольная звезда, которая стро­ится аналогично пятиконечной звезде, как продолже­ние сторон правильного шестиугольника)

октаграмма (восьмиугольная звезда)

декаграмма (десятиуголь­ная звезда)

Ну раз так хорошо вы знаете латинский и греческий, тогда вам не составит труда перевести на русский следующее:

 

Перевод

 

1.	Геометрия		Земля + измеряю, землеизмерение
2.	Тетраэдер		Четыре основания (грани)
3.	Проекция		Бросание вперед
4.	Радикал		Коренной
5.	Трапеция		Столик
6.	Линия	лат	Лен, льняная нить
7.	Конус		Сосновая шишка
8.	Цилиндр	греч	Валик, каток
9.	Хорда	греч	Струна
10.	Призма		Отпиленный кусок
11.	Гексаэдр		Куб, шестигранник
12.	Математика	греч	Познание, наука
13.	Параллельность	греч	Рядом идущий
14.	Биссектриса	лат	Надвое рассекающая
15.	Вектор	лат	Везущий, несущий
16.	Арифметика	греч	Число
17.	Гипербола	греч	Прохожу через что-либо
18.	График	греч	Начертанный
19.	Плюс	лат	Больше
20.	Минус	лат	Меньше
21.	Сфера	греч	Шар
22.	Квадрат	лат	Четырехугольый
23.	Радиус	лат	Спица в колесе
24.	Диаметр	греч	Поперечник
25.	Диагональ	лат	Идущий от угла к углу

 

 АРХИМЕД

(ок. 287-212 до н. э.)

Об Архимеде-великом математике и механике-известно больше, чем о других ученых древности. Прежде всего достоверен год его смерти — год падения Сиракуз, когда ученый погиб от руки римского солдата. Впрочем, историки древности Полибий, Ливии, Плутарх мало рассказывали о его математических заслугах, от них до наших времен дошли сведения о чу­десных изобретениях ученого, сделан­ных во время службы у царя Гиерона II. Этому ученому царь Гиерон II поручил проверить честность юве­лира, изготовившего золотой ве­нец. При этом нельзя было нару­шить целостность изделия. Открыв при принятии ванны закон вытал­кивающей силы, ученый справился с заданием. Именно ему принадле­жит восклицание: «Эврика!», что значит: «Нашел!» Другая легенда рассказывает, что он же соорудил систему блоков, с помощью кото­рой один человек смог спустить на воду огромный корабль «Сиракосия». Крылатыми стали произне­сенные тогда им слова: «Дайте мне точку опоры, и я поверну Землю». Инженерный гений Архимеда с осо­бой силой проявился при осаде Си­ракуз, богатого торгового города на острове Сицилия.

Воины римского консула Марцелла были надолго задержаны у стен го­рода невиданными машинами: мощ­ные катапульты прицельно стреляли каменными глыбами, в бойницах бы­ли установлены метательные маши­ны, выбрасывающие грады ядер, бе­реговые краны поворачивались за пределы стен и забрасывали кораб­ли противника каменными и свин­цовыми глыбами, крючья подхваты­вали корабли и бросали их вниз с большой высоты, системы вогну­тых зеркал поджигали корабли. Как только римляне замечали, что из-за крепостной стены показы­вается веревка или бревно, они об­ращались в бегство с криком, что вот Архимед еще выдумал новую машину на их погибель.

Огромен вклад Архимеда и в раз­витие математики. Он разработал методы на­хождения площадей поверхностей и объе­мов различных фигур и тел, дал об­разцы применения математики в естест­вознании и технике. Автор многих изобре­тений (Архимедов винт, определение со­става сплавов взвешиванием в воде, системы для поднятия больших тяжестей, военные метательные машины и др.).  Архимед много занимался и проб­лемой квадратуры круга. Ученый вы­числил отношение длины окружности к диаметру (число π). Архимед нашел также сумму бес­конечной геометрической прогрессии со знаменателем 1/4. В математике это был первый пример бесконеч­ного ряда.

Большую роль в развитии мате­матики сыграло его сочинение «Псаммит» — «О числе песчинок», в котором он показывает, как с по­мощью существовавшей системы счисления можно выражать сколь угодно большие числа.

 

Вопрос:

 

На могильной плите Архимеда, по его завещанию, был изображен цилиндр с вписанным шаром, а эпита­фия гласила о величайшем открытии Архимеда, что объемы этих тел относятся как 3:2. Когда римский оратор и общественный деятель Цицерон был на Сицилии (в I в. до н. э.), он еще видел заросший кустарником памятник с шаром и цилиндром.

 

А смогли бы вы решить задачи учеников Архимеда без расчетов?

Вопросы, которые я вам задам вза­имосвязаны друг с другом.

 

Вопрос: Сколько нужно проде­лать операций, чтобы засунуть бе­гемота в холодильник?

 

Таких операций три;

первая — нужно открыть холодиль­ник; вторая — положить туда беге­мота; третья — закрыть холодиль­ник.

 

1. Вопрос: Сколько нужно проделать операций, чтобы поместить в холодильник жира­фа?

( 4. Для того, чтобы поместить в холодильник жирафа, нужно проделать не три, а четыре операции. Первая — открыть холодильник; вторая — извлечь из него бегемота; третья — поместить в холодильник жирафа; четвертая — закрыть холодильник.)

 

2. Бегемот и жираф находятся на суше на расстоянии одного километра от берега реки. Вопрос: Кто быстрее добежит до воды?

(Быстрее до берега реки добежит бегемот, так как жираф сидит в холо­дильнике)

 

3. Вопрос: Сколько бегемотов помещается в кузове пятитонного грузовика?

      (В кузове пятитонного грузовика помещается ровно пять тонн бегемо­тов)

 

4. Вопрос: Сколько жирафов поместится в кузове того же грузовика?

(Жирафов в кузове не поместится ни одного, так как весь кузов заполнен бегемотами.)

 

 

ЕВКЛИД

Древнегреческий математик,  рабо­тал в Александрии в III в. до н. э. Главный труд «Начала» (15 книг), содержащий ос­новы античной математики, элементар­ной геометрии, теории чисел, общей тео­рии отношений и метода определения площадей и объемов, включавшего эле­менты теории пределов, оказал огромное влияние на развитие математики. Работы по астрономии, оптике, теории музыки.

В течение двух тысяч лет геометрию узнавали либо из «Начал» Евклида, либо из учебников, написанных на основе этой книги. Лишь про­фессиональные математики обращались к трудам других великих греческих геоме­тров: Архимеда, Аполлония — и геометров бо­лее позднего времени. Классическую геоме­трию стали называть евклидовой в отличие от появившихся в XIX в. «неевклидовых гео­метрий».

Об этом поразительном человеке история сохранила настолько мало сведений, что не­редко высказываются сомнения в самом его существовании. Что же дошло до нас? Евклид должен быть старше Архимеда, ко­торый ссылался на «Начала». До наших вре­мен дошли сведения, что он преподавал в Александрии, и преподавал он, вероятно, четыре науки: арифметику, геометрию, теорию гармонии, астрономию. Кроме «На­чал» до нас дошли книги Евклида, посвя­щенные гармонии и астрономии.

Что касается места Евклида в науке, то оно определяется не столько собственными его научными исследованиями, сколько педагоги­ческими заслугами. Величайшая заслуга Евклида в том, что он подвел итог построению гео­метрии и придал изложению столь совершен­ную форму, что на две тысячи лет «Начала» стали энциклопедией геометрии.

Знаменита его задача «Мост для ослов» — так она называется, не решив которой, по мнению Евклида, нельзя себя считать разумным человеком. Состоит она из доказательств того, что углы при основании равнобедренного треугольника равны.

 

А сейчас – математическое развлечение: попробуем  поиграть в древнейшую игру «Крестики-нолики».

Игра «крестики-нолики» — одна из древней­ших, ее знают все. В квадрате, разделенном на девять клеток, игроки по очереди ставят  в свободную клетку свой знак: крестик или, нолик, стараясь выстроить три крестика или , три нолика подряд. Тот, кто первым сделает  это, выигрывает. Если не делать ошибок, то игра оканчивается вничью, выиграть можно только в том случае, если противник ошибется. Самый правильный первый ход — занять угловую клетку. И если партнер не ответит на это своим знаком в центре, то он проиграл.

Гораздо интереснее усложненный вариант, «крестиков-ноликов» — игра «четыре в ряд». На листке клетчатой бумаги двое играющих по очереди ставят крестики и нолики. Выигрывает игрок, который первым выставит четыре своих знака подряд по вертикали, горизонта­ли   или  диагонали.

 

Ньютон Исаак  

(1643—1727)

Анг­лийский математик, механик, астроном и физик, создатель классической механики. В 1665 г. Исаак Ньютон окончил Кембриджский университет и соби­рался начать работу там же, в его родном Тринити-колледже. Однако чума, бушевавшая в Англии, заста­вила Ньютона уединиться на своей ферме, в Вулсторпе. «Чумные кани­кулы» затянулись почти на два года. Тогда  и сделал молодой уче­ный почти все свои открытия в фи­зике и математике. Он открыл за­кон всемирного тяготения и присту­пил с его помощью к исследова­нию планет. Но чтобы исследовать и выражать законы физики, Ньютону приходи­лось заниматься и математикой. В Вулсторпе Ньютон, решая задачи на проведение касательных к кривым, вычисляя площади криволинейных фигур, создает общий метод решения таких задач-метод флюксий (про­изводных) и флюэнт, которые у Г. В. Лейбница назывались дифферен­циалами. Ньютон вычислил произ­водную и интеграл любой степенной функции. Об этом ученый под­робно пишет в своей самой значи­тельной работе по математике «Ме­тод флюксий» (1670-1671), которая была опубликована уже после его смерти. В ней были заложены основы математического анализа. Ньютон также находит формулу для различ­ных степеней суммы двух чисел (см. Ньютона бином). Когда Ньютон вернулся в Кемб­ридж в 1666 г., он привез бесчис­ленные и бесценные результаты сво­их математических занятий в Вул­сторпе. У него пока не  было  времени привести их в форму, пригод­ную для публикации, и он не то­ропится с этим. Дел у него при­бавляется, в 1669 г. он получает фи­зико-математическую кафедру. В 1672 г. его выбирают членом Лон­донского королевского общества (ан­глийской Академии наук).

В 1688 г. И. Ньютона выбирают в парламент, а в 1699 г. он переез­жает в Лондон, где получает по­жизненное место директора монет­ного двора.

Работы И. Ньютона надолго опре­делили пути развития физики и ма­тематики. Значительная часть клас­сической механики надолго сохрани­лась в виде, созданном Ньютоном. Закон всемирного тяготения посте­пенно осознавался как единый прин­цип, позволяющий строить совершен­ную теорию движения небесных тел. Созданный им математический ана­лиз открыл новую эпоху в матема­тике.

 

Лобачевский Николай Ивано­вич

(1792—1856)  

 

Российский математик, создатель неевклидовой геометрии (гео­метрии Лобачевского). Открытие Ло­бачевского (1826, опубликовано 1829— 1830), не получившее признания совре­менников, совершило переворот в пред­ставлении о природе пространства, в основе которого более двух тысяч лет ле­жало учение Евклида, и оказало огромное влияние на развитие математического мышления. Труды по алгебре, математи­ческому анализу, теории вероятностей, механике, физике и астрономии – вот перечень его интересов.

Откры­тие в Казани гимназии побудило вдову Прасковью Але­ксандровну Лобачевскую к переезду в Казань. В ноябре 1802 г. П. А. Лобачевская возбудила ходатайство о приня­тии трех ее сыновей — Александра одиннадцати лет, Ни­колая девяти и Алексея семи лет, в гимназию на казен­ное содержание. При этом она оговорила, что при отсут­ствии вакансий она просит принять их на собственное ее содержание. В то время было в обычае, что родители детей, принимаемых в гимназию, вносили единовремен­ное пожертвование в пользу гимназии. П. А. Лобачев­ская в своем прошении указала, что по своей бедности она такого взноса сделать не может. Однако совет гимна­зии 5 (17) ноября 1802 г. постановил принять всех трех мальчиков на казенное содержание. Вступительные экзамены в гимназию были не просты — об этом можно судить по при­водимым ниже воспоминаниям С. Т. Аксакова, по той радости, с которой его родители приняли известие, что сын их выдержал экзамен и принят на казенное содер­жание. Хорошо подготовить детей к экзаменам Пра­сковье Александровне, которая сама была едва грамотна, было отнюдь не легко. Но то обстоятельство, что все три ее сына были приняты «казеннокоштными» воспитан­никами, свидетельствует об их хорошей подготовке. Во всяком случае, в возрасте девяти лет Лобачевский поступил в пансион Казанской гимназии вместе со своими братьями и в    дальнейшем и семье проводил только короткие каникулярные проме­жутки; он был, таким образом, предоставлен школьным воспитателям и самому себе.

Жизнь гимназии в этот период, как уже сказано, ярко описана С. Т. Аксаковым. Он поступил в гимназию раньше Лобачевского: был зачислен казеннокоштным воспитанни­ком в первый класс в декабре 1800 г. и оставлен в нем в пансионе. В своих «Воспоминаниях» он пишет, что режим в гимназии был очень суровый. «Вставание по звонку задолго до света при по­тухших   и   потухающих   сальных   свечах,   наполнявших воздух нестерпимой вонью; холод в комнатах, отчего вста­вать было еще неприятнее… Общественное умывание из медных рукомойников, около которых всегда бывает ссора и драка; ходьба на молитву, к завтраку, к обеду и т. д.». Но не в этой, может быть до некоторой степени необходимой, дисциплине   общежития   была   суть  дела. Гораздо хуже было то полное подавление личности воспи­танника,   которое  последовательно  проводилось  со  дня его поступления в гимназию до окончания ее… По распо­ряжению   гимназического   начальства   никто   из   воспи­танников не мог иметь у себя ни своих вещей, ни денег. Деньги, если они были, хранились у комнатных надзира­телей и употреблялись с разрешения главного надзирателя; покупка   съестного   и   лакомства   строго   запрещалась; конечно, были злоупотребления, но под большой тайной.

Н. И. Лобачевский учился очень хорошо, аттестовался — «весьма прилежным и благонравным» и уже в конце гимна­зического курса «занимающимся с особенным прилежа­нием математикой и латинским языком». Сам Лобачевский рассказывал, что когда он был гимназистом, один из его учителей, выведенный из себя его буйным характером, вскричал: «Ты, Лобачевский, будешь разбойником!» Наиболее значительно то, что при скромной подготовке, которую они могли получить дома у матери, все три брата Лобачевские успешно справлялись с учением и прошли курс гимназии без задержек, не оставаясь на второй год. Хорошо известно, с каким трудом усваиваются в школе языки, а между тем уже в начале обучения  в университете  Лобачевский был в состоянии читать научные мемуары на латинском, немецком и французском языках. Содержа­ние математических мемуаров, которые он штудировал, настолько серьезно, что с ними и в настоящее время справился бы только хорошо подготовленный студент, а Лоба­чевскому в то время было всего 15 лет.

В январе 1807 г Лобачевский окончил первую «Kaзанскую»  гимназию  и  поступил  в  Казанский  университет. Вся жизнь Н.И. Лобачевского была связана с Казанским универ­ситетом. С 1814 г. Лобачевский утвержден адъютантом физико-математических наук  приступил к преподаванию  в университете: читает лекции по ма­тематике, физике, астрономии, заве­дует обсерваторией, возглавляет биб­лиотеку. В течение нескольких лет он избирался деканом физико-мате­матического факультета.

Еще в первых числах февраля 1826 г. он передал в университет ру­копись «Сжатое изложение начал гео­метрии со строгим доказательством теоремы о параллельных»,  речь здесь шла о построении геометрии. Вероятно, ни­кто из присутствовавших не мог ус­ледить за ходом мысли Лобачевско­го. Созданная комиссия из членов Совета несколько лет не давала за­ключения.

В 1830 г. в «Казанском вестнике» выходит работа «О началах геомет­рии», представляющая собой извле­чение из доклада на Совете. Чтобы разобраться в ситуации, решили вос­пользоваться помощью столицы: в 1832 г. статью послали в Петербург. И здесь никто ничего не понял, ра­бота была квалифицирована как бес­смысленная. Не следует слишком су­рово судить русских ученых: нигде в мире математики еще не были готовы воспринять идеи неевклидо­вой геометрии.

Ничто не могло поколебать уве­ренность Лобачевского в своей пра­воте. В течение 30 лет он продол­жает развивать свою геометрию, пы­тается делать изложение более до­ступным, публикует работы по-фран­цузски и по-немецки.

Немецкую версию изложения про­читал Гаусс и, разумеется, понял автора с полуслова. Он прочитал его работы на русском языке и оце­нил их в письмах к ученикам, но публичной поддержки новой геомет­рии Гаусс не оказал.

Н. И. Лобачевский дослужился до высоких чинов, он был награжден большим числом орденов, пользо­вался уважением окружающих, но о его геометрии предпочитали не го­ворить, даже в те дни, когда Ка­зань прощалась с ним. Прошло еще не менее двадцати лет, прежде чем геометрия Лобачевского завоевала права гражданства в математике.

 

Шахматная задача

А сейчас я хочу знакомить всех присут­ствующих с тем, какой интерес­ный с математической точки зре­ния случай произошел в древней Индии с изобретателем шахмат.

Шахматы — одна из самых древних игр. Она существует уже многие века, неудивительно, что с нею связаны предания, правди­вость которых за давностью вре­мени невозможно проверить. Од­ну из подобных легенд вы сейчас услышите. Чтобы понять ее, вовсе необязательно уметь играть в шахматы.

Достаточно знать, что вся игра происходит на доске, разграфлен­ной на 64 клетки, и что эти клетки белые и черные.

Итак, повторяю, что шахмат­ная игра была придумана в Индии изобретателем по имени Сета.

 Когда индийский Царь Шерам познакомился с шахматами, он был восхищен остроумием этой игры и ее разнообразием.

Давайте подслушаем это историческое событие:

 

ЦАРЬ: Я восхищен этой новой игрой — шахматами. Кто ее изоб­ретатель?

ПРИДВОРНЫЙ: Один из ва­ших подданных, о, великий Царь. Зовут его Сета. (Указывает.) Вот он.

ЦАРЬ: Пусть Сета приблизится. Я желаю достойно вознагра­дить тебя, Сета, за прекрасную иг­ру, которую ты придумал.

СЕТА: Я счастлив, великий Царь, что сумел обрадовать вас. ЦАРЬ: Я достаточно богат, чтобы исполнить самое смелое твое пожелание. Назови награду. Не робей, выскажи свою просьбу. Я не пожалею ничего, чтобы вы­полнить ее.

СЕТА: Велика доброта твоя, о, повелитель. Но я так робею, бо­юсь, что мое желание покажется слишком дерзким.

ЦАРЬ: Я дал обещание и вы­полню его. Говори!

СЕТА: Повелитель, прикажи мне выдать за первую клетку шах­матной доски I пшеничное зерно.

ЦАРЬ: Простое пшеничное зерно?

СЕТА: Да, повелитель. За вто­рую клетку прикажи выдать 2 зер­на, за третью — 4, за четвертую — 8, за пятую — 16, за шестую — 32.

ЦАРЬ: Я понял, ты хочешь по­лучить награду зернами пшени­цы. Так, чтобы число зерен удваи­валось за каждую клетку? И это все?

СЕТА: Да, повелитель.

ЦАРЬ: Довольно! Ты полу­чишь свои зерна за все 64 клетки доски, согласно твоему желанию: за каждую вдвое больше предыду­щей. Но знай, что твоя просьба недостойна моей щедрости. Про­ся такую ничтожную награду, ты непочтительно пренебрегаешь моей милостью. Поистине, ты бы мог показать лучший пример ува­жения к доброте твоего государя. Ступай, мои слуги вынесут тебе твой мешок с пшеницей.

(Сета кланяется, улыбается и ухо­дит.)

Придворный! Пусть немедлен­но сосчитают, какова величина награды, потребованной этим изобретателем, и выдадут ему мешок.

(Придворный уходит. Выходит Слуга с опахалом в руках и начинает обма­хивать Царя.)

ВЕДУЩИЙ: За обедом Царь вспомнил об изобретателе шах­мат и пожелал узнать, унес ли тот свою жалкую награду.

(Входит Придворный.)

ЦАРЬ: Придворный! Подсчи­тан ли размер награды для Сеты?

ПРИДВОРНЫЙ: Повелитель, приказание твое исполняется. Придворные математики исчис­ляют число следуемых зерен.

ЦАРЬ (гневно): Почему мое приказание до сих пор не выпол­нено! Я не привык, чтобы мои приказания исполнялись так медленно!

ВЕДУЩИЙ: Вечером, от­правляясь ко сну, Царь еще раз осведомился, подсчитан ли раз­мер награды для Сеты.

ЦАРЬ: Придворный! Давно ли Сета со своим мешком пшеницы покинул дворец?

ПРИДВОРНЫЙ: Повелитель, счетоводы твои трудятся без уста­ли и надеются, что еще до рассве­та закончат подсчет.

ЦАРЬ: Почему медлят? Завт­ра, прежде, чем я проснусь, все до последнего зерна должно быть выдано Сете! Я дважды не прика­зываю.

ВЕДУЩИЙ: Рано утром к Ца­рю явились с докладом.

ЦАРЬ: Прежде, чем ты ска­жешь о своем деле, я желаю ус­лышать, выдана ли, наконец, Сете та награда, которую он себе назначил?

ПРИДВОРНЫЙ: Ради этого я и осмелился явиться перед тобой в столь ранний час. Мы добросо­вестно исчислили все количество зерен, которое желает получить Сета. Число это так велико…

ЦАРЬ: Как бы ни было оно велико, житницы мои не оскуде­ют. Награда обещана и должна быть выдана.

ПРИДВОРНЫЙ: Не в твоей власти, повелитель, исполнять подобные желания. Во всех амба­рах твоих нет такого числа зерен, какое потребовал Сета. Нет его и в житницах целого царства. Не найдется такого числа зерен и на всем пространстве земли. Но ес­ли ты желаешь выдать обещан­ную награду, то прикажи осу­шить моря и океаны, превратить земные царства в пахотные поля, прикажи растопить льды и снега, покрывающие далекие северные пустыни. Пусть все то простран­ство будет сплошь засеяно пше­ницей. И все то, что родится на этих полях, прикажи отдать Сете. Тогда он получит свою награду.

ЦАРЬ: Назови же мне это чу­довищное число!

ПРИДВОРНЫЙ: 18 квин­тильонов 446 квадрильонов 744 триллиона 73 биллиона 709 мил­лионов 551 тысяча 615, о, пове­литель! (Кланяется.)

18 446 744 073 709 551 615

(Царь в ужасе замирает. Придвор­ный, Царь и Слуга входят за кули­сы.)

ВЕДУЩИЙ: Вот это награда! Конечно, она не могла бы быть выдана, ведь только амбар для хранения такого гигантского ко­личества зерна должен прости­раться на расстояние, вдвое большее, чем расстояние от Зем­ли до Солнца.

Решить эту задачу мы попросим этих молодых людей!

 

Математики – живые люди, они любили, боролись, им ставили памятники.

Нильс Генрих Абель

(1802-1829)

 

В Королевском парке в Осло стоит скульптура сказочного юноши, по­пирающего двух поверженных чудо­вищ; по цоколю идет надпись «ABEL».

Что же символизируют чудовища? Первое из них, несомненно, — алгебра­ические уравнения 5-й степени. К тому времени Абель был уже студентом университета в Осло (тог­да Христиании). Он был совершенно лишен средств к существованию, и первое время стипендию ему выпла­чивали профессора из собственных средств. Затем он получил государст­венную стипендию, которая позволи­ла ему провести два года за гра­ницей. В Норвегии были люди, ко­торые понимали, сколь одарен Абель, но не было таких, кто мог бы по­нять его работы. Будучи в Герма­нии, Абель так и не решился посе­тить К. Гаусса.

Представленный в академию «Мемуар об одном очень общем классе трансцендентных функций» не был рассмотрен, рукопись Абеля была обнаружена через сто лет. (В скульптуре эту работу олицетворяло второе поверженное чудовище.) Абель не знал, что 30 лет назад в этих вопросах далеко продвинулся Гаусс,   но   ничего   не   опубликовал.

 

Эварист Галуа

(1811-1832)

Он прожил двадцать лет, всего пять лет из них занимался математикой. Математические работы, обессмер­тившие его имя, занимают чуть бо­лее 60 страниц.

В 15 лет Галуа открыл для себя математику и с тех пор, по словам одного из преподавателей, «был одер­жим демоном математики». Юноша отличался страстностью, неукроти­мым темпераментом, что постоян­но приводило его к конфликтам с окружающими, да и с самим собой.

Ему было неполных 18 лет, когда была опубликована его первая работа. И в те же годы Галуа два раза подряд не удается сдать экзамены в Политехническую школу, самое престижное учебное за­ведение того времени. В 1830 г. он был принят в привилегированную Высшую нормальную школу, гото­вившую преподавателей. За год уче­бы в этой школе Галуа написал несколько работ; одна из них, посвя­щенная теории чисел, представляла исключительный интерес.

Бурные июльские дни 1830 г. заста­ли Галуа в стенах Нормальной шко­лы. Его все более захватывает но­вая страсть — политика. Галуа присо­единяется к набиравшей силы рес­публиканской партии — Обществу дру­зей народа, — недовольной политикой Луи-Филиппа. Возникает конфликт с директором школы, всеми сила­ми противодействовавшим росту по­литических интересов у учащихся, и в январе 1831 г. Галуа исключают из школы. В январе 1831 г. Галуа передал в Парижскую академию наук рукопись своего исследования о ре­шении уравнений в радикалах.  Однако академия отвергла работу Га­луа — слишком новы были изложен­ные там идеи. В это время Галуа находился в тюрьме. После освобож­дения уже в июле он вновь ока­зывается в тюрьме Сент — Пелажи пос­ле попытки организовать манифеста­цию 14 июля (в годовщину взятия Бастилии), на сей раз Галуа приго­ворен к 9 месяцам тюрьмы. За ме­сяц до окончания срока заключения заболевшего Галуа переводят в боль­ницу. В тюрьме он встретил свое двадцатилетие.

29 апреля он выходит на свобо­ду, но ему было суждено прожить еще лишь только один месяц. 30 мая он был тяжело ранен на дуэли. На следующий день он умер. В день перед дуэлью Галуа написал своему другу Опосту Шевалье письмо: «Пуб­лично обратись к Якоби или Гаус­су с просьбой дать мнение не об истинности, а о значении тех теорем, развернутого доказательства кото­рых я не даю, и тогда, надеюсь, кто-нибудь сочтет полезным разоб­раться во всей этой путанице». Ра­боты Галуа содержали окончатель­ное решение проблемы о разреши­мости алгебраических уравнений в ра­дикалах, то, что сегодня называется теорией Галуа. Дру­гое направление в его исследовани­ях связано с так называемыми абелевыми интегралами и сыграло важ­ную роль в математическом анали­зе XIX в. Работы Галуа были опуб­ликованы лишь в 1846 г., а признание к ним пришло еще позже.

 

Марков Андрей Андреевич

(1856-1922)

 А. А. Марков-русский математик, представитель петербургской мате­матической школы. Он родился в Рязани. В 1874 г. поступил на физико-математический факультет Петер­бургского университета, где занялся теорией непрерывных дробей и тео­рией чисел.

В 1884 г. Марков защитил док­торскую диссертацию, посвященную непрерывным дробям, в которой до­казал и обобщил некоторые нера­венства опубликованные раньше без доказательств. Маркову принадлежат также многочисленные работы по различным разделам ма­тематического анализа. В 1890 г. за глубокие научные исследования Мар­ков был избран академиком Петер­бургской академии наук.

С конца 90-х гг. XIX в. главным предметом исследований ученого стала теория вероятностей. Здесь он ввел новый объект исследования — последовательности зависимых случайных величин, полу­чившие в дальнейшем название мар­ковских цепей. А. А. Марков был страстным и убежденным борцом против произ­вола и несправедливости царского режима, выступал против попыток подчинить преподавание математики в школе религиозным взглядам. Он отказался от царских орденов, подал в Синод просьбу об отлучении от церкви, указав в ней, что не со­чувствует всем религиям, которые, подобно православию, поддержи­ваются огнем и мечом и сами слу­жат им. Резкие выпады против веры в чудеса содержатся в учебнике А. А. Маркова «Исчисление вероят­ностей», опубликованном в дорево­люционное время. После выхода кни­ги ученого обвинили в безбожии и «подрыве основ». От преследова­ний его избавил лишь крах царского режима.

 

 

Ведущий:

У нас готов ответ? Ну, тогда дадим еще несколько минут за которые все остальные решат геометрическую задачку:

 

СОВЕТ МУДРЕЦА

Один из афоризмов легендарного Козьмы Пруткова гласит: «Бросая в воду камешки, смотри на круги, ими образуемые, иначе такое бросание будет пустой заба­вой». Это высказывание родилось на берегу пруда со стоячей водой.

Вопрос: Как меняется форма волны, если камешки бросать в речку?

 

Ответ:

Если вода не течет, то волны, возникающие в ней, — круговые. При наличии течения все точки этой волны под­вергаются параллель­ному переносу, причем все точки переносятся по параллельным прямым с одинаковой скоростью. Совершенно понятно, что та­кой перенос не меняет форму волны и она остается круговой.

 

 

Карл Фридрих Гаусс

(1777-1855)

 Король математики. Математические вычисления замени­ли Гауссу обычные детские игры.

Девятнадцатилет­ний Гаусс окончательно решил за­ниматься математикой (до этого он не мог сделать выбор между мате­матикой и филологией). И всего че­рез 9 дней в его дневнике появ­ляется запись об открытии. Гаусс доказал так называемый квад­ратичный закон взаимности — один из основных в теории чисел. Этот за­кон открыл еще Л. Эйлер, но дока­зать его не смог.

С именем К. Ф. Гаусса связаны многие замечательные страницы в истории математики. Он дал дока­зательство основной теоремы алгеб­ры (всякое алгебраическое уравне­ние с действительными коэффициен­тами имеет корень). Гаусс создал теорию поверхностей. До него были изучены геометрии только на двух поверхностях: на плоскости (плани­метрия Евклида) и на сфере (сфери­ческая геометрия). Гаусс нашел спо­соб построения геометрии на лю­бой поверхности, определил, какие линии играют на поверхности роль прямых, как мерить расстояния меж­ду точками на поверхности и т.д. Теория Гаусса получила название внутренней геометрии. Он не опуб­ликовал своих работ по неевклидо­вой геометрии и теории эллипти­ческих функций. Эти результаты бы­ли открыты заново его младшими современниками: русским математи­ком Н. И. Лобачевским и венгерским математиком Я. Больяй — в первом случае и норвежским математиком Г. X. Абелем и немецким математи­ком К. Г. Якоби – во втором. Ему уда­лось вычислить орбиту малой пла­неты (астероида) Цереры.                               Решение этой сложной задачи принесло уче­ному известность, и он был пригла­шен заведовать кафедрой матема­тики и астрономии, с которой бы­ла связана должность директора Геттингенской обсерватории. Этот пост Гаусс не покидал до конца жизни. Результаты своих исследований по астрономии Гаусс объединил в фун­даментальном труде «Теория движе­ния небесных тел».

 

Готфрид Вильгельм Лейбниц

(1646-1716)

 

Математика не была его единствен­ной страстью. Он был философом и лингвистом, историком и биологом, дипломатом  и политическим деятелем, математиком и изобретателем. Научные и об­щественные планы Лейбница были грандиозны. Он мечтал о создании всемирной академии наук, о построе­нии «универсальной науки». Он хотел выделить простейшие понятия, из которых по определенным правилам можно сформировать все сколь угод­но сложные понятия. Лейбниц меч­тал об универсальном языке, позво­ляющем записывать любые мысли в виде математических формул, при­чем логические ошибки должны про­являться в виде математических оши­бок. Он думал о машине, которая выводит теоремы из аксиом, о пре­вращении логических утверждений в арифметические (эта идея была воп­лощена в жизнь в нашем веке).

Но грандиозность замыслов ужи­валась у Лейбница с пониманием того, что может быть непосредствен­но осуществлено. Он не может ор­ганизовать всемирную академию, но в 1700 г. организует академию в Берлине, рекомендует Петру I орга­низовать академию в России. При организации Петербургской Акаде­мии наук в 1725 г. пользовались пла­нами Лейбница. Он прекрасно умеет решать конкретные задачи и в мате­матике: создает новый тип арифмо­метра, который не только складывает и вычитает числа, но и умножает, де­лит, возводит в степень и извлекает квадратные и кубические корни, ре­шает трудные геометрические задачи. Вводит понятие определителя и за­кладывает основы теории определи­телей. В отличие от Ньютона Лейбниц по­тратил много сил на передачу своего метода другим математикам, среди которых выделялись братья Якоб и Иоганн Бернулли. По его инициативе создается журнал, в котором группа математиков оттачивает методы но­вого математического анализа.

Ученый, занимавшийся разработ­кой универсального языка, понима­ет, какую роль в новом исчислении должна играть символика. Кста­ти, Лейбниц предложил несколько математических знаков, на­пример = (равенство), • (умножение).

 

МАТЕМАТИЧЕСКИЕ ЗНАКИ

 

Математические  знаки — условные обозначе­ния, которые служат для записи математиче­ских понятий. Развитие системы обозначений в математике было тесно связано с общим развитием ее по­нятий и методов.

Первыми математическими знаками были цифры. В работах древнегреческих математи­ков, например в «Началах» Евклида, отрезки и другие геометрические объекты обознача­лись буквами. Зачатки буквенного обозначе­ния величин появились в III в., когда Диофант ввел обозначения для неизвестной величины и ее степеней, предложил особые знаки для операции вычитания и для обозначения равен­ства. Буквенные обозначения для неизвестных применяли индийские математики в VII в., од­нако создание развернутого буквенного исчис­ления относится к XIV-XVII вв. В конце XV в. француз Н. Шюке и итальянец Л. Пачоли впервые написали знаки сложения и вычита­ния р и т (от латинского plus и minus), а не­мецкие математики ввели современные обо­значения  +  и  —.

В XVI в. математики применяли смешанные записи, содержавшие слова и некоторые мате­матические знаки.

 

Ребята, я попрошу подойти ко мне 5 добровольцев. Я вам раздам 5 математических записей. Попробуйте их прочесть.

В итоге должно получиться, уравнение х³ +  5х = 12

                                             

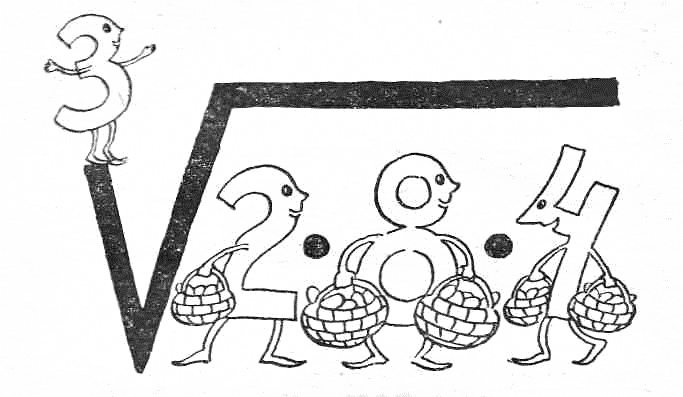
 Алгеброгорск

ЭВОЛЮЦИЯ ЗАПИСИ УРАВНЕНИЯ

 

 

Вопрос:

В начале XVII в. три математика абсолютно автономно придумывают и внедряют в употребление один знак. Итальянский математик Р. Бомбелли  предло­жил  квадратный вариант, круглый — итальянский математик Н. Тарталья, а фигурный — Ф. Виет. Все три варианта были приняты и мы используем их до сир пор, прибавив еще и вертикальный вариант. Что это за знак? (Скобки)

 

 

ЖЕНЩИНЫ-МАТЕМАТИКИ

 Мало было в прошлом ученых-женщин, еще меньше — женщин-математиков. Первая женщина-математик, согласно дошедшим до нас сведениям, была гречанка Гипатия, жившая в Александрии от 370 до 415 года. Гипатия изучала математику, астрономию, медицину и фило­софию, написала комментарии к «Арифметике» Диафанта и к «Коническим сечениям» Апполония Пергского. Она была красива, красноречива, обаятельна; ее мнение и советы не только в облас­ти науки и литературы, но и в практической жизни ценились все­ми. Среди ее знакомых и друзей было много христиан, однако сама она была язычницей и оставалась верной традициям своих пред­ков. Однажды, когда Гипатия возвращалась домой, толпа фана­тиков-христиан, подстрекаемых александрийским епископом, по­тащила ее к церкви и убила, забрасывая камнями. Затем ее тело было разорвано на куски и сожжено. В истории многих веков после смерти Гипатии не сохранилось никаких сведений об уче­ных-женщинах.

В первой половине XVIII в. во Франции славилась своей обра­зованностью маркиза Эмилия де Шатлэ, которая перевела с ла­тинского на родной язык знаменитое произведение Ньютона «Ма­тематические начала натуральной философии». Это грандиозный труд, в котором изложены учение о всемирном тяготении и прин­ципы классической механики.

Другая французская женщина XVIII в., Мария Лаланд, сов­местно со своим братом и мужем составила тригонометрические таблицы, известные под названием «Таблицы Лаланд». Как способ­ная вычислительница была известна также француженка Гортен­зия Лепот. Отметим, что ее именем был назван декоративный цве­ток, привезенный ею из Индии.

Более   яркими   математическими   способностями   и   эрудицией обладала итальянка Мария Гаетана Аньези (1718—1799),   которая была первой в мире женщиной,   занимавшей   должность   профес­сора математики в  Болонском  университете. Она написала «Курс анализа   для   употребления   итальянского    юношества»,    в   котором  даны оригинальные доказательства многих теорем, а также гео­метрический трактат. В ее честь одна из кривых линий, ею иссле­дованных,   поныне   называется   «кривой   Аньези».

Англичанка  Мэри  Сомервиль  (1780—1872)   вела  переписку с выдающимися учеными, среди которых были Гей-Люссак, Лаплас, Араго и др. Она написала несколько книг по астрономии и физики  и   перевела   на  родной   язык   знаменитое   произведение  Лапласе  «Небесная механика». Ее ученица, Ада Байрон (1815—1852), единственная дочь известного английского поэта Дж. Байрона, творчество которого так любили Пушкин,  Лермонтов и  Белинский, тоже  занималась  математикой,   и  в  частности   математическими  машинами.

Глубоким творческим талантом  обладала  француженка Софья Жермен   (1776—1831).    Так  как   родители   не разрешали ей  заниматься математикой, которой она увлекалась с детства, Софья писала свои выкладки тайком, по ночам под одеялом. Однажды, в начале XIX в., она написала всемирно известному немецкому математику К. Ф. Гауссу письмо, в котором содер­жалась просьба разъяснить некоторые недоумения, возникшие в ходе ее математических исследований. Письмо она подписала мужскими именем, так как опасалась, что знаменитый ученый не станет уделять внимание женщине, занимающейся математикой. Гаусс оценил по достоинству своего талантливого незнакомою корреспондента и выразил желание узнать его лично. Случай для этого представился в 1807 г., когда французские войска заняли немецкий город Геттинген, в котором жил Гаусс. Софья просила генерала, командовавшего французскими оккупационными вой­сками, пощадить жизнь Гаусса, дабы его не постигла трагическая судьба великого Архимеда из Сиракуз. Узнав об этом, Гаусс был глубоко тронут всем происшедшим и до конца жизни хранил глу­бокое уважение и дружбу к Жермен.

 

Выдающейся женщиной-математи­ком была

Ковалевская Софья Васильев­на

(1850—1891)

российский математик, первая женщина — член-корреспондент Петербургской АН (1889). Ос­новные труды по математическому анали­зу (дифференциальные уравнения и ана­литические функции), механике (враще­ние твердого тела вокруг неподвижной точки) и астрономии (форма колец Сатур­на). Автор беллетристических произведе­ний (повесть «Нигилистка», опубликована 1892; «Воспоминания детства», 1889, пол­ный текст — 1893).  

Она родилась в Москве 15 января 1850 года в семье артиллерий­ского генерала В. Корвин-Круковского. С раннего детства Софья пристрастилась к чтению литературы и научных книг. Математические ее способности проявились впервые в возрасте   13 лет.

Был у Софьи дядя, Петр Василье­вич, «Хотя он математике никогда не обучался, — пишет Ковалевская, — он питал к этой науке глубочай­шее  уважение.   Из разных   книг   набрался он кое-каких математических сведений и любил пофи­лософствовать по их поводу, причем ему часто случалось раз­мышлять вслух, в моем присутствии. От него услышала я, напри­мер, в первый раз о квадратуре круга, об асимптотах (прямых линиях), к которым кривая постоянно приближается, никогда их не достигая, о многих других вещах подобного рода, смысла которых я, разумеется, понять еще не могла, но которые действовали на мою фантазию, внушая мне благоговение к математике».

Говоря об этих первых моих соприкосновениях с областью ма­тематики, я не могу не упомянуть об одном очень курьезном об­стоятельстве, тоже возбудившем во мне интерес к этой науке. Ког­да мы переезжали на житье в деревню, весь дом пришлось отде­лать заново и все комнаты оклеить новыми обоями. Но так как  комнат было много, то на одну из наших детских комнат, обоев не хватило, а выписывать-то обои приходилось из Петербурга; это было целой историей, и для одной комнаты их выписывать реши­тельно не стоило. Все ждали случая, и в ожидании его эта обиженная комната так и простояла много лет с одной стороны оклеен­ная простой бумагой. Но по счастливой случайности на эту оклей­ку пошли именно листы литографированных лекций Остроград­ского о дифференциальном и интегральном исчислениях, приобре­тенные моим отцом в молодости.

Листы эти, испещренные странными, непонятными формулами скоро обратили на себя мое внимание. Я помню, как я в детстве проводила целые часы перед этой таинственной стеной, пытаясь разобрать хоть отдельные фразы и найти тот порядок, в котором листы должны бы следовать друг за другом. От долгого, ежеднев­ного созерцания внешний вид многих из формул так и врезался в моей памяти, да и самый текст оставил о себе глубокий след в мозгу, хотя в самый момент прочтения он и остался для меня не­понятным.

Когда много лет спустя, уже пятнадцатилетней девочкой, я брала первый урок дифференциального исчисления у известного преподавателя математики в Петербурге, Александра Николаеви­ча Страннолюбского, он удивился, как скоро я схватила и усвоила понятие о пределе и о производной, точно я наперед их знала. Я помню, он именно так и выразился. И дело, действительно, бы­ло в том, что в ту минуту, когда он объяснял мне эти понятия, мне вдруг живо припомнилось, что все это стояло на памятных мне листах Остроградского, и самое понятие о пределе показалось мне давно знакомым».

Увлечение математикой у Ковалевской было настолько силь­ным, что она забыла обо всем остальном. В те времена в России, и в большинстве стран Запада, женщинам не был разрешен доступ в высшие учебные заведения. Для поездки за границу требовалось,  чтобы женщина была замужем. Софья в возрасте 18 лет вышла за­муж за В. О. Ковалевского. С мужем Софья Васильевна уехала в Германию. С большим трудом ей удалось поступить в Гейдельбергский университет, где она слушала лекции по высшей математике, физике и другим наукам. Однако Ковалевская стремилась в Бер­линский университет, одним из профессоров которого был выдаю­щийся математик Карл  Вейерштрасс. Так как и в Берлинский университет женщины доступа не имели, Софья Васильевна отпра­вилась к Вейерштрассу на дом и просила его, чтобы он занимался с нею частным образом. Чтобы отвя­заться от необычной просительницы, Вейерштрасс предложил ей решить несколько очень трудных задач. Оказалось, однако, что С. Ковалев­ская их быстро решила. Убедившись в исключительных способностях сво­ей посетительницы, Вейерштрасс со­гласился заниматься с нею.

После четырех лет занятий с Вейерштрассом и большой настой­чивой работы С. Ковалевская смогла представить три научных труда Геттингенскому университету, который присудил ей сте­пень доктора «с высшей  похвалой».

Вернувшись в Россию, Ковалевские поселились в Петербурге. На родине Софья Ковалевская не могла применить свои знания: женщинам научная карьера была закрыта. В 1878 г. она родила дочь, за этим последовала длительная ее болезнь. Но и по выздоровлении С. Ковалевская достойной работы найти не могла. Царский министр просвещения, отвечая отказами на все ходатайства Софьи Васильевны, выразился при этом, что она и ее дочь «успеют состариться прежде, чем женщин будут допускать  к  университету».

В 1883 г. умер В. О. Ковалевский. После смерти мужа Софья Васильевна надолго уединилась, стремясь забыться в математи­ческих исследованиях.

В конце 1883 г. она по приглашению старого друга и бывшего ученика Вейерштрасса, профессора Миттаг-Леффлера, заняла долж­ность доцента, а вскоре и профессора Стокгольмского универ­ситета. Она с большим подъемом читала лекции по различным разделам высшей математики. Многие студенты и преподаватели с любовью ее называли «наш профессор Соня».

Самой важной научной работой С. Ковалевской было полное решение задачи о вращении тяжелого твердого тела вокруг непод­вижной точки. За эту работу ей была присуждена в 1888 г. премия Парижской академии наук.

Несмотря на успехи и почести, С. Ковалевская чувствовала себя одинокой на чужбине и глубоко тосковала по Родине. Ковалевская знала французский, английский, немецкий и шведский языки, однако считала, что самые сокровенные свои мысли может выра­жать только на своем родном, на русском языке. Она всю жизнь мечтала о том, чтобы преподавать, работать у себя на родине, однако даже после ее научных успехов в царской России для нее места не нашлось. Президент Петербургской академии наук, ве­ликий князь Константин Константинович ответил на ходатайства Чебышева и других русских ученых о предоставлении Кова­левской соответствующего места следующим образом: «Так как доступ на кафедры в наших университетах совсем закрыт для жен­щин, каковы бы ни были их способности и познания, то для   г-жи Ковалевской в нашем отечестве нет места столь же почетного и хорошо    оплачиваемого,   как то,   которое она занимает в Стокгольме».

В последние годы своей жизни Софья Ковалевская подружилась со шведской писательницей Эллен Кэй и вновь увлеклась ли­тературной деятельностью, работая над повестью о великом рус­ском революционном демократе и писателе Н. Г. Чернышевском, В конце января 1891 г. по дороге из Франции в Швецию она сильно простудилась и заболела воспалением легких, 10 февраля 1891 г,  в полном расцвете творческих сил Софья Васильевна скончалась.

                  После С. Ковалевской в самом начале XX в. другие две русские  женщины   получили в Геттингенском   университете  степень  доктора за труды в области математики, а именно Надежда Нико­лаевна Гернет, преподававшая потом в Петербурге на высших жен­ских курсах, и Любовь Николаевна Запольская, работавшая на тех же курсах в Москве.

 

Дважды два – четыре

Капитаны!

Настал ваш час показать   свои   математические способности.

1. Загадайте число до 10 (кроме 0)
2. Умножаем на 9
3. Складываем числа этого числа
4. Вычитаем 4
5. Под этим порядковым числом в алфавите есть буква. На эту букву загадайте страну
6. На третью букву этой страны загадайте животное

Не гоните, капитаны, в Дании носороги не водятся!

 

ВЕДУЩИЙ: Мы с вами окуну­лись в таинственный и прекрасный мир математики. Желаем вам не только извлекать пользу из занятий этой удивительной наукой, но и восхищаться ее красотой.

 

 

На всякий случай:

ПИФАГОР И ЕГО УЧЕНИЕ

В списке величайших математиков от древности до наших дней на первом месте стоит имя Пифагора. О его жизни известно немного. Он родился около 570 г. до н. э. на ионийском острове Самосе. Отцом Пифа­гора называют Мнесарха, известного камнереза. В

поисках знаний Пифагор покинул родной остров. Он побывал почти во всех эллинских городах, многих стра­нах. Учился у халдейских мудрецов, персидских магов, египетских жре­цов. В Южной Италии, в Кротоне, он основал знаменитую школу пифаго­рейцев, исповедующую его тайное учение.

Вопросы:

1. Как называлась система знаний пифагорейской школы?
2. Что являлось символом принадлежности к школе Пифагора?
3. Теорема Пифагора о том, что в прямоугольном треугольнике сумма площадей квадратов, построен­ных на катетах, равна площади квадрата, построенно­го на гипотенузе, была известна в Вавилонии уже во времена Хаммурапи (в XVIII веке до н. э., т. е. за двенадцать веков до рождения Пифагора). Почему же она носит имя Пифагора?
4. Какие величайшие открытия были сделаны Пифагором?

 

Ответ:

1. Система знаний пифагорейской школы называ­лась «математа» (от этого названия и пошло название науки математика). Она состояла из четырех частей: арифметики, геометрии, астрономии и учения о гар­монии.
2. Символом принадлежности к пифагорейской шко­ле была пятиконечная звезда, считавшаяся в то время и символом здоровья.
3. Эта теорема названа в честь Пифагора потому, что ее доказательство приписывается Пифагору. Сейчас неизвестно ни то, как он ее доказывал, ни то, принад­лежит ли это доказательство Пифагору или кому-то из его учеников, потому что свои^открытия пифагорейцы держали в тайне.
4. К величайшим открытиям, сделанным Пифагором, относится, наряду с доказательством теоремы для прямоугольного треугольника, и доказательство несо­измеримости отрезков, т. е. существования иррацио­нальных чисел. Предание гласит, что за раскрытие тайны существования иррациональных чисел пифаго­реец Гиппас был покаран богами: Он утонул при кораблекрушении.

 

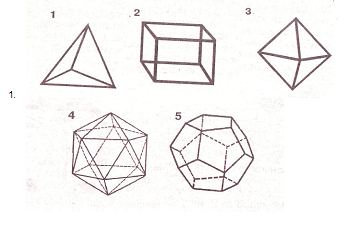
 ПЛАТОНОВЫ ТЕЛА

Известна шутка английского геометра Томпсона Д. о том, что «Евклид вовсе не собирался выпускать систе­матический учебник геометрии. Он задался целью написать сочинение о правильных многогранниках, рассчитанное на начинающих, в силу чего ему при­шлось изложить все необходимые сведения». Евклид считал венцом своего творения именно последнюю книгу «Начал» — тринадцатую, в которой помещены способы построения с помощью циркуля и линейки пяти Платоновых тел.

 

Вопросы:

1. Что такое Платоновы тела?
2. Какие правильные многоугольники можно постро­ить с помощью циркуля и линейки и кем была доказана теорема о том, что не любой правильный многоуголь­ник можно построить с помощью циркуля и линейки?
3. Какое наибольшее число сторон имеет правиль­ный n-угольник, методика построения которого раз­работана на сегодняшний день?

 

Ответы:

1. Платоновы тела — это пять правильных многог­ранников: тетраэдр (1), куб (2), октаэдр (3), икосаэдр (4), додекаэдр (5). Тетраэдр, куб, додекаэдр были известны Пифагору, который привел способ вписать их в сферу. Октаэдр и икосаэдр были открыты Теэтетом. Он же доказал, что других правильных выпуклых тел не существует. В философии Платона тетраэдр символизировал огонь, куб — землю, октаэдр — воз­дух, икосаэдр — воду, додекаэдр — вселенную.

КВАДРАТУРА КРУГА

Нахождение квадратуры круга — задача, которой более 20 веков.

Вопросы: Могли бы вы сформулировать, что означа­ет найти квадратуру круга, и почему эта задача нераз­решима?

Ответ:

«Найти квадратуру круга» — значит начертить квад­рат, площадь которого равна площади заданного кру­га, пользуясь циркулем и линейкой. Невозможность решения этой задачи строго была доказана в 1882 г. профессором Мюнхенского университета Карлом Лин­де маном. Трудность состоит не в том, что я — ирра­циональное число, так как можно с помощью линейки и циркуляра строить отрезки, превышающие заданные в иррациональное число раз, например, в V2 ,автом, что число я является трансцендентным числом, т. е. оно не является решением какого-либо алгебраического урав­нения. Именно это и было доказано Линдеманом.

 

 

«ЮМОРИСТИЧЕСКАЯ ПАУЗА»

СЦЕНКА 1

УЧИТЕЛЬ: Как разделить на шестерых пять картошек? ВОВА: Надо сделать пюре.

СЦЕНКА 2

УЧИТЕЛЬ: По дороге одна за другой идут семь коров. Кото­рая из них может обернуться и сказать: «Я вижу шесть пар ро­гов?»

«ЮМОРИСТИЧЕСКАЯ ПАУЗА»

УЧИТЕЛЬ:   Вова,  что  так круг?

ВОВА: Это квадрат, у которс~ нет ни одного угла.

А чтобы быть точно уверенной, что вы действительно математики, сейчас я проверю вас на внимательность и смекалку.

Класс – 5

Круто – 4

Ништяк – 3

Отдохни– 2  

 

 

Задание

Шел Кондрат в Ленинград,

А навстречу — двенадцать ребят.

У каждого по три лукошка,

В каждом лукошке — кошка,

У каждой кошки — двенадцать котят.

У каждого котенка

В зубах по четыре мышонка.

И задумался Кондрат:

«Сколько мышат и котят

Ребята несут в Ленинград?»

 

(0. В Ленинград шел только Конд­рат, остальные шли в обратную сторону.)